Основные теоретические положения
Важное свойство ДПТ с независимым возбуждением от постоянных магнитов состоит в том, что результирующий момент сил от всех проводников якоря, называемый электромагнитным моментом двигателя M, пропорционален току якоря Iя, потребляемому двигателем от источника питания:
,
где km - коэффициент пропорциональности, называемый постоянной момента двигателя. Его размерность [Нм/А]. По законам электромагнитной индукции в проводнике, движущемся в магнитном поле, возникает электродвижущая сила. Суммарная ЭДС катушек якоря E через коллектор и щетки прикладывается к внешним выводам двигателя. В двигательном режиме работы эта ЭДС направлена против внешнего напряжения Uя, подведенного к якорю от источника питания. Поэтому ЭДС двигателя часто называется противоЭДС. Она прямо пропорциональна угловой скорости вращения вала двигателя wдв[рад/с]:
,
где kω - коэффициент пропорциональности, называемый постоянной ЭДС двигателя. Его размерность [Вс/рад].
Природа электромагнитных явлений в ДПТ такова, что если
используется система единиц СИ, то значения коэффициентов kω и km численно равны.
Уравнения, описывающие электрические процессы в ДПТ
В электрической якорной цепи двигателя протекает ток Iя под действием напряжения постоянного тока Ua источника питания и противоЭДС двигателя.
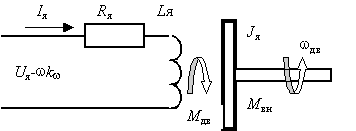Рис. 1
Эта цепь характеризуется параметрами: активным сопротивлением Rя [Ом] и индуктивностью Lя[Гн] якорной обмотки. Вращающийся ротор, обладающий моментом инерции Ja[Нм с2/рад], приводится в движение одновременным действием электромагнитного момента двигателя Mдв и момента внешних сил Mвн, приложенного к валу двигателя.
Исходные дифференциальные уравнения ДПТ составляются на основании законов физики. Для электрической цепи используется второй закон Кирхгофа, согласно которому можно записать уравнение
,
где член RяIя характеризует падение напряжения на активном сопротивлении якорной цепи в соответствии с законом Ома, а член Lя(dIя/dt) отражает наличие ЭДС самоиндукции, возникающей в обмотке при изменении тока якоря. В представленном уравнении не учитывается падение напряжения на щетках, зависящее нелинейно от тока якоря, но имеющее, как правило, относительно небольшое значение по сравнению с напряжением Uя.
Дифференциальное уравнение, характеризующее процессы в механической части двигателя, составляется на основании второго закона Ньютона:
,
где Mвн - момент внешних сил, действующий относительно оси вращения вала двигателя. В этом уравнении не учитывается действие сил трения, возникающих при вращении ротора, но оказывающих относительно слабое действие на ускорение вала ДПТ.
Используя вышеприведенные формулы и приводя дифференциальные уравнения к нормальной форме Коши, получим описание ДПТ в форме:
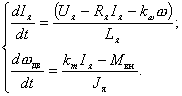
Для исследования процессов с помощью ЭВМ удобно использовать структурное представление математической модели ДПТ. Для этого преобразуем полученную систему линейных дифференциальных уравнений по Лапласу при нулевых начальных условиях. В результате получим систему алгебраических уравнений:
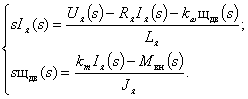
в которых s - переменная Лапласа, а величины Iя(s), wдв(s), Uя(s), Mвн(s) - изображения по Лапласу переменных Iя, wдв, Uя, Mвн соответственно. После эквивалентных преобразований эти уравнения могут быть представлены в форме:
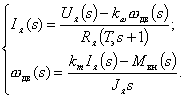
где Тэ = Lя/Rя - электромагнитная постоянная времени якорной цепи двигателя.
По уравнениям с помощью системы SIMULINK может быть сформирована структурная схема ДПТ для его математического моделирования (рис.1).
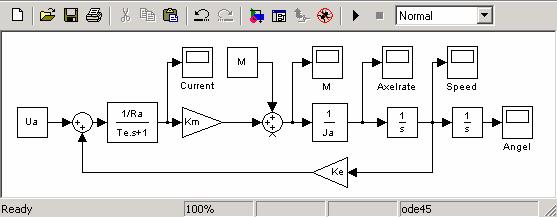
Рис. 1
Важным параметром ДПТ, определяющим его динамические свойства, является электромеханическая постоянная времени двигателя:
.
Зависимость между электромагнитным моментом двигателя и частотой вращения ротора в установившемся режиме при постоянных Uя и Mвн называется механической характеристикой двигателя. Уравнение механической характеристики имеет вид:
.
При пуске двигателя, когда скорость равна нулю, развивается пусковой момент
.
Частота вращения вала двигателя при отсутствии сопротивления называется
частотой вращения холостого хода
.